How Does The Resultant Displacement Change As The Angle Between Two Vectors Increases From 0 To 180
Vectors and Projectiles
Navigate to:
Review Session Abode - Topic Listing
Vectors and Projectiles - Home || Printable Version || Questions and Links
Answers to Questions: All || #1-ix || #10-45 || #46-55 || #56-72
[ #10 | #11 | #12 | #13 | #14 | #fifteen | #16 | #17 | #18 | #19 | #xx | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #thirty | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 ]
Part B: Multiple Choice
ten. If 2 displacement vectors of 6 meters and viii meters (with varying directions) are added together, then the resultant could range anywhere between ___ meters and ___ meters.
| a. 0, 48 | b. 1.33, 48 | c. 0, 14 | d. 2, 14 |
| e. ... nonsense! No such prediction tin be made. | |||
| f. ... nonsense! A prediction can be made only none of these choices are correct. | |||
Answer: D
The vector sum of 6.0 meters and eight.0 meters volition exist the greatest if they are added together in the same direction; that would produce a resultant of xiv meters. The vector sum of vi.0 meters and 8.0 meters volition be the smallest if they are added together in the contrary management; that would produce a resultant of ii.0 meters. An blitheness depicting the various resultants of vi.0 meters added to 8.0 meters at varying directions is shown on a separate page. See blitheness .
11. Three vectors are added following the rules of vector add-on. A fourth vector is drawn from the tail of the first vector to the head of the final vector. This fourth vector is referred to equally ____.
| a. the equilibrant | b. the hypotenuse | c. the resultant | d. a mistake |
Answer: C
The resultant represents the result of adding two or more vectors. On a scaled vector add-on diagram, the resultant is ever drawn from the tail of the beginning vector to the head of the last vector.
12. TRUE or Faux:
The order in which vectors is added will effect the finish result.
Respond: B
The order in which vectors is added does not effect the magnitude or direction of the resultant. A + B + C gives the aforementioned resultant as B + C + A and the same resultant every bit A + C + B. An animation depicting the the head-to-tail addition of five vectors in three different orders is shown on a split folio. See blitheness .
13. Vector A is directed northward and vector B is directed eastward. Which of the following vector addition diagrams best stand for the addition of vectors A and B and the subsequent resultant?
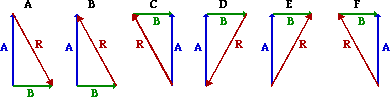
Reply: Due east
If the head-to-tail method (sometimes referred to as the triangle method) is being used, then the tail of B should be drawn starting at the head of A. Both diagrams D and E show this. So the resultant should be drawn from the tail of A to the head of B (which is not shown in diagram D). There is also a parallelogram method for calculation vectors. In this method, the tails of the two vectors are placed together (as in diagrams A and B). So a parallelogram should be drawn with the two vectors forming the adjacent sides of the parallelogram. The resultant is drawn from the tails of the vectors to the reverse corner of the parallelogram. This is not done correctly on diagrams A and B. Diagrams C and F exercise non resemble any (accurate) vector improver method known to humankind.
14. When adding vector B to vector A geometrically (or graphically) using the head to tail method, the resultant is drawn from ____ to the ____.
| a. head of A, tail of B | b. tail of A, head of B | ||
| c. caput of B, tail of A | d. tail of B, caput of A |
Reply: B
Adding vector B to vector A is equivalent to saying A + B. In such an instance, A is drawn starting time, so B is drawn with its tail at the head of A. Finally, the resultant is drawn from the tail of the start vector (A) to the head of the terminal vector (B).
Use the following vector improver diagrams for Questions #xv-#20.
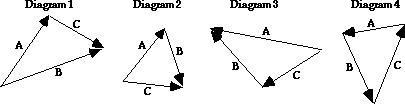
xv. Which 1 of the following vector addition equations is shown in Diagram 1?
| a. A + B = C | b. A + C = B | c. B + C = A | d. B + A = C |
| e. C + B = A | f. C + A = B | m. None of these |
sixteen. Which i of the following vector addition equations is shown in Diagram ii?
| a. A + B = C | b. A + C = B | c. B + C = A | d. B + A = C |
| eastward. C + B = A | f. C + A = B | g. None of these |
17. Which i of the post-obit vector addition equations is shown in Diagram three?
| a. A + B = C | b. A + C = B | c. B + C = A | d. B + A = C |
| e. C + B = A | f. C + A = B | g. None of these |
18. Which 1 of the following vector addition equations is shown in Diagram iv?
| a. A + B = C | b. A + C = B | c. B + C = A | d. B + A = C |
| e. C + B = A | f. C + A = B | g. None of these |
Answers to questions #15-#xviii:
15. B
16. A
17. E
18. G
Vectors are added past a head-to-tail method and the resultant is fatigued from the tail of the outset vector to the head of the last vector. So if ii vectors are added - say B is added to A (as in A + B) - and then start A is drawn and the tail of B is placed at the head of A. The resultant is drawn with its tail at the tail of A and its head at the head of B. Thus, when the tails of two vectors are seen connected, one of the vectors is the resultant and the other is the first vector being added. And when the heads of two vectors are seen continued, one of the vectors is the resultant and the other is the second vector beingness added. These principles can be applied to answer the in a higher place questions.
Note that in question 18, there is not a single vector which is fatigued from the tail of one vector to the caput of another vector. Thus, no resultant is drawn. 1 could say that the diagram shows that A + B + C = 0.
19. Consider the magnitude and direction of vectors A and B equally shown in Diagram ane higher up. Which 1 of the following diagrams would correspond B - A = R?
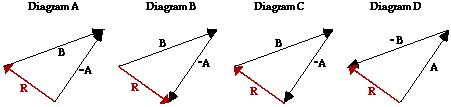
Answer: B
The subtraction of A from B is equivalent to calculation the negative of A to B. That is, B - A = B + (-A). The negative of a vector is simply the same vector drawn in the opposite management. The correct respond should exist a diagram which shows B being fatigued first. Then at the head of B, the tail of a vector pointing in the contrary direction of A should be drawn. This is shown in both diagrams B and C. The resultant should so be drawn from the tail of B to the caput of -A. This is non shown in diagram C.
20. Consider the magnitude and direction of vectors B and C as shown in Diagram 2 above. Which ane of the following diagrams would stand for C - B = R?
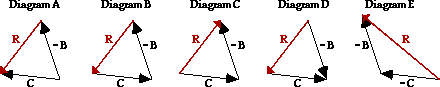
Answer: C
The subtraction of B from C is equivalent to adding the negative of B to C. That is, C - B = C + (-B). The negative of a vector is simply the same vector fatigued in the contrary direction. The correct respond should be a diagram which shows C being drawn outset. Then at the head of C, the tail of a vector pointing in the reverse direction of B should exist drawn. This is shown in both diagrams B and C. The resultant should then be drawn from the tail of C to the caput of -B. This is not shown in diagram B.
21. The vector sum (magnitude but) of 25.0 m, n + 18.0 one thousand, East is ___ thou.
| a. vii.00 | b. 21.5 | c. 30.8 | d. 35.8 |
| e. 43.0 | f. 54.ii | g. 949 | h. None of these |
Answer: C
These two vectors are directed at right angles to each other. In such instances, the vector sum can be determined using the Pythagorean theorem. The resultant (R) is equal to the foursquare root of the sum of the squares of the two vectors beingness added. That is, R = Sqrt (A2 + B2) where A and B are the two vectors being added together. Thus,
R = 30.805 m = ~30.eight m
22. The vector sum (magnitude merely) of 32.0 yard, north + 41.0 m, due west is ___ m.
| a. 9.00 | b. 36.5 | c. 38.0 | d. 52.0 |
| e. 73.0 | f. 128 | m.2.lxx 10 103 | h. None of these |
Answer: D
Like question #21 higher up, these ii vectors are directed at right angles to each other. The Pythagorean theorem can be used to make up one's mind the resultant of their sum. The resultant (R) is equal to the square root of the sum of the squares of the two vectors being added.
R = Sqrt [ (32.0 m)ii + (41.0 grand)2 ] = Sqrt [ (1024 gii) + (1681 thou2) ] = Sqrt (2705 m2)
R = 52.010 m = ~52.0 m
Use the diagram below to reply Questions #23-#28. Each foursquare on the diagram represents a 20-meter x 20-meter expanse.
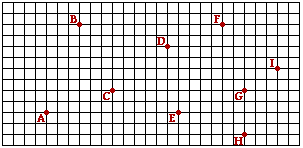
23. If a person walks from D to H to One thousand to C, so the distance walked is ____ meters.
| a. 128 | b. 180 | c. 401 | d. 460 |
| e. 480 | f. 533 | thousand. 620 | h. None of these |
Answer: F
Altitude is a scalar quantity and adding together 3 scalars is every bit simple as adding the three numbers arithmetically. However, since the first of the 3 legs of this trip is not due East, West, North or Due south, determining the distance for this leg requires that the Pythagorean theorem is used. That is, walking from D to H is equivalent to walking 140 meters east (vii squares) and 160 meters (8 squares) south. The distance from D to H is thus 212.6 meters - Sqrt [ (140 m)ii + (160 m)2 ]. The walk from H to M is a altitude of 80 meters (4 squares) and the walk from G to C is 240 meters (12 squares). The total altitude walked is the sum of 212.half-dozen m + 80 m + 240 m = 532.half-dozen thou = ~533 g.
24. If a person walks from D to H to Chiliad to C, so the magnitude of the displacement is ____ meters.
| a. 128 | b. 180 | c. 401 | d. 460 |
| due east. 480 | f. 533 | m. 620 | h. None of these |
Reply: A
Displacement is a vector quantity which indicates how far our of identify an object is at the end of the motion relative to the beginning of the motion. Deportation does not depend upon the path taken from the get-go position to the final position, only but upon the distance of a vector fatigued from start to finish. The resultant for the three segments of this walk is merely drawn from D to C. The distance of this resultant is constitute by using the Pythagorean theorem. The resultant stretches south 80 meters (iv squares) and westward 100 meters (five squares). The resultant has a magnitude of Sqrt [ (80 grand)2 + (100 k)ii ] or 128 meters.
25. If a person walks from D to H to G to C, then the management of the deportation is ___ degrees (every bit measured counterclockwise from Eastward).
| a. 39 | b. 51 | c. 53 | d. 217 |
| e. 219 | f. 231 | g. 233 | h. None of these |
Answer: Eastward
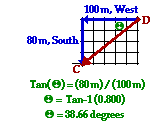As discussed in the previous problem, the resultant stretches south 80 meters (4 squares) and west 100 meters (5 squares). This is shown in the diagram at the right. These 2 parts of the resultant vector can be combined with a trigonometric function to determine the angle theta. The bending theta is approximately 38.7 degrees. This is not the direction of the resultant displacement merely simply the angle between the deportation vector and due West. The convention used to express the direction of the vector is to mensurate the counterclockwise bending of rotation from due Due east. So in this instance, the direction is 180 degrees + 38.7 degrees or ~219 degrees.
26. If a person walks from H to E to C to Yard, then the distance walked is ____ meters.
| a. eighty. | b. 240. | c. 253 | d. 333 |
| eastward. 493 | f. 560. | chiliad. 640. | h. None of these |
Answer: E
Distance is a scalar quantity and adding together three scalars is as simple as adding the individual distances of the 3 legs is as unproblematic equally adding the distances. arithmetically. The problem is simplified in that the first two legs of the trip are forth the same line segment. The stop at E tin can be overlooked since its is merely a bespeak on the line from location H to location C. That is HE + EC = HC. Since the HC line segment does non stretch not east, Westward, North or S, determining the altitude for this leg requires that the Pythagorean theorem is used. That is, walking from H to C is equivalent to walking 240 meters west (12 squares) and lxxx meters (iv squares) north. The altitude from D to H is thus 253.0 meters - Sqrt [ (240 m)2 + (80 g)two ]. The walk from H to E to C is a distance of 253 meters and the walk from C to G is 240 meters (12 squares). The full altitude walked is the sum of 253 grand + 240 m = ~493 yard.
27.
If a person walks from H to E to C to G, so the magnitude of the displacement is ____ meters.
| a. fourscore. | b. 240. | c. 253 | d. 333 |
| e. 493 | f. 560. | g. 640. | h. None of these |
Answer: A
Displacement is a vector quantity which indicates how far our of place an object is at the end of the motion relative to the first of the motility. Displacement does not depend upon the path taken from the first position to the terminal position, but only upon the distance of a vector drawn from start to terminate. The resultant for the three segments of this walk is simply drawn from H to Grand. The altitude of this resultant is merely 80 meters (iv squares), north.
28. If a person walks from H to E to C to G, and so the direction of the deportation is ___ degrees (every bit measured counterclockwise from E).
| a. 0 | b. 18. | c. 72 | d. 90. |
| e. 108 | f. 162 | 1000. 342 | h. None of these |
Answer: D
The last destination Thousand is due Due north of the initial location. Thus, the displacement is directed north (at 90 degrees).
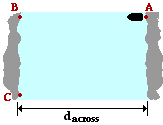
Use the following diagram for Questions #29-#33. In the diagram, a riverboat is shown starting at position A on the east depository financial institution of a river. The boat heads towards position B (a point directly beyond the river from A) with a speed of 3.8 grand/s. But because of a current with a speed of one.eight yard/s, the boat lands on the west banking concern of the river at position C, a location downstream from B. The width of the river (dacross) is 86.four meters.
29. The magnitude of the resultant velocity of the boat is ____ m/s.
| a. 1.eight | b. 2.0 | c. 3.iv | d. 3.eight |
| eastward. iv.2 | f. 5.vi | grand.11 | h. None of these |
Answer: Due east
This is a case of a boat crossing a river past use of its motor. The motor allows the boat to travel iii.8 meters towards the opposite shore in every second. The river is flowing south, carrying the boat a altitude of ane.viii meters downwardly the river every 2d. The resultant velocity is simply the vector sum of these two individual velocities. Since these two velocities are at correct angles to each other, the vector sum can be adamant using the Pythagorean theorem.
vresultant = Sqrt[ (3.eight thou/s)two + (ane.8 thou/southward)2 ]
vresultant = 4.2 m/s
30. The direction of the resultant velocity of the boat is ____ m/due south.
| a. 0 | b. xviii. | c. 712 | d. 90. |
| e. 108 | f. 162 | g. 342 | h. None of these |
Answer: H
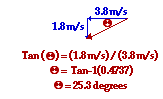The direction of the resultant velocity is in a southeastern direction. That puts the vector in the third quadrant with a direction somewhere betwixt 180 degrees and 270 degrees. The verbal bending tin can be determined if the bending theta is found using trigonometry. Theta is the angle that the resultant velocity (the red vector in the diagram at the correct) makes with due Due west. This bending can exist constitute suing the tangent function. The work is shown at the right.
The angle theta is found to be 25.three degrees. The bodily management as measured as the counterclockwise angle of rotation with due East is 180 degrees plus 25.3 degrees. This would be 205.3 degrees.
31. The time required for the gunkhole to cross the 86.4 m wide river is ___ seconds.
| a. 4.2 | b. 15 | c. 21 | d. 23 |
| e. 48 | f. None of these |
Answer: D
The motor allows the gunkhole to travel 3.8 meters towards the opposite shore in every 2nd. The boat has 86.4 meters to travel from shore to shore. (The presence of the current does non alter the width or shore-to-shore distance.) The time to cantankerous the river can be calculated from the river width and the boat velocity using the v = d/t equation. Rearranging the equation to solve for t yields
t = (86.four thou) / (3.8 grand/southward) = ~23 south (unrounded 22.7 s)
32. Location C is the location where the boat ultimately lands on the opposite shore. What is the distance from location B to location C.
| a. 37 | b. 41 | c. 78 | d. 86 |
| e. 96 | f. 180 | yard. 2.0 x 10two | h. None of these |
Answer: B
The distance that location C is downstream from B is mathematically related to the speed of the river and the fourth dimension to cross the river. The distance can be calculated by multiplying the electric current speed past the fourth dimension to cross the river.
ddownstream = (1.eight m/southward) • (22.vii s)
ddownstream = ~41 yard
33. If the current on a particular twenty-four hours was flowing with ii times the velocity, then the time to cross the river would be ____.
| a. two times greater | b. one-half as corking | ||
| c. greater, merely not two times greater | d. less, but not one-half the original time | ||
| e. the same equally it was when the current flowed at i.8 grand/s. | |||
Answer: East
For this situation of a boat heading straight across the river, the current velocity is directed perpendicular to the boat velocity. These two components of the boats resulting motion are independent of each other. The boat velocity makes the sole contribution to the ability of the gunkhole to cross the river. The river velocity only carries the boat southward down the river. So an amending of the river velocity would accept no effect on the time required for the boat to cross the river.
34. An object is undergoing gratis fall motion. Every bit it falls, the object'due south ____.
| a. speed increases | b. acceleration increases |
| c. both of these | d. none of these |
Answer: A
As an object gratis-falls, its velocity (and as well its speed) changes by approximately ten chiliad/southward every 2nd. This means that the acceleration is a constant value of 10 m/s/s. An object has a changing speed (or velocity) and a constant dispatch if the speed changes past the aforementioned amount (a "constant amount") in each sequent second of its motility.
35. A football is kicked into the air at an bending of 45 degrees with the horizontal. At the very top of the brawl'due south path, its velocity is _______.
| a. entirely vertical | b. entirely horizontal |
| c. both vertical and horizontal | d. not enough data given to know. |
Respond: B
As a projectile rises towards its summit, its horizontal velocity remains abiding while its vertical velocity decreases. At its peak, its vertical velocity becomes 0 thousand/s. At this instant in fourth dimension, the velocity is entirely horizontal; there is no vertical component to the velocity.
36. A football is kicked into the air at an angle of 45 degrees with the horizontal. At the very superlative of the ball's path, its acceleration is _______. (Neglect the furnishings of air resistance.)
| a. entirely vertical | b. entirely horizontal |
| c. both vertical and horizontal | d. not plenty information given to know. |
Answer: A
As a projectile rises towards its peak, its horizontal velocity remains constant while its vertical velocity decreases. This is to say that the acceleration of the object is vertical, not horizontal. At the tiptop and everywhere throughout the trajectory, there is a vertical (downward) dispatch. In fact, a projectile is an object upon which the only strength is gravity. This force causes an acceleration which is in the same direction as the strength - downward.
37. A football is kicked into the air at an angle of 45 degrees with the horizontal. At the very acme of the ball'south path, the net force interim upon it is _______. (Neglect the effects of air resistance.)
| a. entirely vertical | b. entirely horizontal |
| c. both vertical and horizontal | d. not plenty information given to know. |
Answer: A
A projectile is an object upon which the merely force is gravity. Since no other forces human activity upon the object, the cyberspace force would be downward.
38. At what point in its path is the horizontal component of the velocity (vx) of a projectile the smallest?
| a. The instant it is thrown. | b. Halfway to the top. | c. At the peak. |
| d. As it nears the top. | e. It is the same throughout the path. | |
Answer: Eastward
As a projectile rises towards its elevation, its horizontal velocity remains constant while its vertical velocity decreases. This is to say that the dispatch of the object is vertical, not horizontal. Having a constant horizontal velocity, there is no betoken along the trajectory where the vten value is smaller than at other points.
39. At what point in its path is the vertical component of the velocity (vy) of a projectile the smallest?
| a. The instant it is thrown. | b. Halfway to the top. | c. At the top. |
| d. As it nears the top. | e. Information technology is the same throughout the path. | |
Answer: C
Equally a projectile rises towards its peak, its horizontal velocity remains constant while its vertical velocity decreases. During the upward portion of its trajectory, the vy continuously decreases until it becomes 0 yard/s at the peak. Thus, the vy is as small equally it will ever be when it is at the peak of the trajectory.
forty. An aeroplane that flies at 100 km/h in a 100 km/h hurricane crosswind has a speed (relative to the ground) of ____.
| a. 0 km/h | b. 100 km/h | c. 141 km/h | d. 200 km/h |
Respond: C
When an object such as a aeroplane or a boat moves within a medium which is moving relative to the ground, the speed of the plane or boat (as measured by its speedometer) will not be the same every bit the speed as measured past a person on the ground (ground speed). The basis speed (i.due east., resultant velocity produced past the combination of the airplane's speed and the wind speed) can be adamant by adding the plane speed and wind speed equally vectors. In this case, the two vectors are at right angles, then the resultant velocity tin exist adamant using the Pythagorean theorem.
R = SQRT( (100 km/60 minutes)2 + (100 km/hr)ii )
R = 141 km/hr
41. An airplane moves at 141 km/h toward the northeast (45 degrees). What is its component velocity in the n direction?
| a. 41 km/h | b. 100 km/h | c. 110 km/h | d. 141 km/h |
Answer: B
To make up one's mind the component of a vector in a given direction, vector resolution principles must be applied. This velocity vector is directed at 45 degrees and has magnitude of 141 km/hr. The vertical component (northward) of this vector tin can be found using the sine role.
vy = (141 km/hour)*sine(45 degrees)
vy = 100 km/hr
42. Ringlet a bowling ball off the edge of a table. Equally information technology falls, its horizontal component of velocity ___.
| a. decreases | b. remains constant | c. increases |
Respond: B
Once the ball leaves the table'south border, information technology becomes a projectile. As it falls, its horizontal velocity remains constant while its vertical velocity decreases. This is to say that the dispatch of the object is vertical, not horizontal. In fact, a projectile is an object upon which the only forcefulness is gravity. This strength causes an dispatch which is in the aforementioned direction as the force - downward.
43. A bullet is fired horizontally and hits the basis in 0.5 seconds. If it had been fired with twice the speed in the same management, it would accept hit the ground in ____. (Assume no air resistance.)
| a. less than 0.5 s. | b. more than than 0.v s. | c. 0.5 due south. |
Respond: C
In one case the bullet leaves the cage, it becomes a projectile (bold no air resistance). Equally it falls, its horizontal velocity remains constant while its vertical velocity decreases. The forcefulness of gravity acts upon the bullet to cause its downward acceleration. The movement of the bullet in the downward direction is independent of the motion in the horizontal direction. That is to say, any amending in a horizontal attribute of its motion will not effect the move in the vertical direction. The time to fall vertically to the ground is not effected by the horizontal speed of the projectile. Information technology would still accept 0.5 seconds to fall to the ground from this peak regardless of the horizontal speed.
44. A projectile is launched at an bending of 15 degrees above the horizontal and lands down range. For the aforementioned speed, what other projection angle would produce the same downrange distance?
| a. 30 degrees. | b. 45 degrees. | c. l degrees. | d. 75 degrees | due east. 90 degrees. |
Answer: D
For projectiles launched at angles, a launch angle of 45 degrees will provide the largest horizontal displacement. Any two launch angles which are separated from 45 degrees by the same corporeality (for case, 40 degrees and l degrees, xxx degrees and 60 degrees and 15 degrees and 75 degrees) volition provide the aforementioned horizontal displacement.
45. 2 projectiles are fired at equal speeds but different angles. 1 is fired at bending of thirty degrees and the other at sixty degrees. The projectile to hit the ground first will be the ane fired at (fail air resistance) ____.
| a. 30 degrees | b. 60 degrees | c. both hit at the same time |
Answer: A
For projectiles launched at angles, a launch angle of 45 degrees will provide the largest horizontal displacement. Launch angles greater than 45 degrees result in big vertical components of velocity; these stay in the air longer and ascension to college heights. Launch angles less than 45 degrees effect in small vertical components of velocity; these practise non rise as high and terminate up falling to the footing in shorter times.
Navigate to:
Review Session Home - Topic Listing
Vectors and Projectiles - Dwelling house || Printable Version || Questions and Links
Answers to Questions: All || #1-ix || #ten-45 || #46-55 || #56-72
You Might Besides Similar ...
Users of The Review Session are frequently looking for learning resource that provide them with exercise and review opportunities that include built-in feedback and educational activity. If that is what you're looking for, and then yous might also like the following:
- The Calculator Pad
The Calculator Pad includes physics give-and-take problems organized past topic. Each problem is accompanied past a pop-up answer and an audio file that explains the details of how to approach and solve the problem. Information technology's a perfect resources for those wishing to ameliorate their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Vectors and Projectiles
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a serial of interactive questioning modules for the educatee that is serious about improving their conceptual understanding of physics. Each module of the serial covers a different topic and is further broken downwardly into sub-topics. A "MOP feel" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like surround. It is available for phones, tablets, Chromebooks, and Macintosh computers. Information technology's a perfect resources for those wishing to refine their conceptual reasoning abilities. Function 1 of the serial includes Vectors and Projectiles.
Visit: MOP the App Home || MOP the App - Part ane
Source: https://www.physicsclassroom.com/reviews/Vectors-and-Projectiles/Vectors-and-Projectiles-Answers-2
Posted by: woodsbobviscep.blogspot.com
0 Response to "How Does The Resultant Displacement Change As The Angle Between Two Vectors Increases From 0 To 180"
Post a Comment